У шкільному зошиті чи в задачнику кожен із нас зустрічав рівнобедрений трикутник. Ця фігура завжди привертає увагу своєю симетрією. А коли доходить до обчислень, перше, що потрібно — це правильно знайти висоту. Саме вона відкриває шлях до площі, кутів та інших важливих елементів.
Що таке висота і чому вона особлива у рівнобедреному трикутнику
Висота — це відрізок, опущений із вершини перпендикулярно до протилежної сторони. У звичайному трикутнику вона може ділити основу як завгодно. У рівнобедреному — все інакше: висота з вершини до основи завжди ділить її навпіл і водночас стає медіаною та бісектрисою.
Уявіть дах будинку з двома однаковими схилами. Якщо провести крокву від верхньої точки прямо вниз, вона опиниться точно посередині. Це і є наочний приклад того, як працює висота.
Ми бачимо, що висота тут — не просто допоміжна лінія, а ключ до симетрії. Коли це розумієш, задачі з геометрії перестають лякати, а починають виглядати логічними.
М’який заклик: спробуйте самі провести висоту на папері — переконаєтесь, як легко перевірити цю властивість.
Формула висоти до основи
Найчастіше потрібно знайти саме висоту, проведену до основи. Якщо позначити основу як bb, а бічну сторону як aa, то висоту можна обчислити через теорему Піфагора:
h = √(a² – (b² / 4))
Приклад. Маємо трикутник із бічними сторонами 10 см і основою 12 см. Висота буде:
h = √(10² – (12² / 4)) = √(100 – 36) = √64 = 8 см.
Інший приклад. Якщо основа 14 см, а бічні сторони по 13 см, тоді:
h = √(169 – (196 / 4)) = √(169 – 49) = √120 ≈ 10,95 см.
Як бачите, формула працює швидко. Кілька хвилин — і ви маєте результат.
М’який заклик: потренуйтеся на власних числах — так формула запам’ятається набагато краще.
Висота до бічної сторони
У рівнобедреному трикутнику можна опустити висоту і на бічну сторону. Тут ситуація складніша: пряма вже не збігається з медіаною чи бісектрисою. Щоб знайти цю висоту, зазвичай використовують площу:
S = ½ * b * h
Знаючи площу і основу, легко знайти висоту. Або навпаки — знаючи висоту, визначити площу.
Приклад. Якщо площа рівнобедреного трикутника 60 см², а основа дорівнює 12 см, то висота:
h = (2 * S) / b = (120) / 12 = 10 см.
Таке рішення часто трапляється у шкільних задачах. Воно показує, як висота стає мостом між різними характеристиками.
М’який заклик: не обмежуйтесь лише формулою — шукайте кілька шляхів розв’язання. Це допоможе швидше зорієнтуватися на контрольній.
Як висота пов’язана з іншими елементами
Висота рівнобедреного трикутника має кілька важливих ролей:
вона допомагає обчислити площу;
ділить основу на дві рівні частини;
у симетричних задачах виступає медіаною і бісектрисою;
часто використовується для знаходження радіуса вписаного чи описаного кола.
Приклад із життя. Якщо ми малюємо декоративний прапорець у формі трикутника, то саме висота допоможе правильно розташувати малюнок чи логотип посередині.
Інший приклад. У задачах з будівництва висота використовується для визначення нахилу ската даху чи довжини балок. Це вже практичний вимір поза шкільними завданнями.
М’який заклик: звертайте увагу на зв’язки — вони роблять геометрію живою і зрозумілою.
Приклади задач із рішеннями
Бічна сторона 5 см, основа 6 см.
h = √(25 – (36/4)) = √(25 – 9) = √16 = 4 см.Основу поділили на відрізки 3 см і 3 см, бічна сторона 5 см.
Вийшов прямокутний трикутник із катетами 3 см і 4 см, тож висота дорівнює 4 см.Якщо площа дорівнює 24 см², а основа 8 см:
h = (2 * 24) / 8 = 6 см.
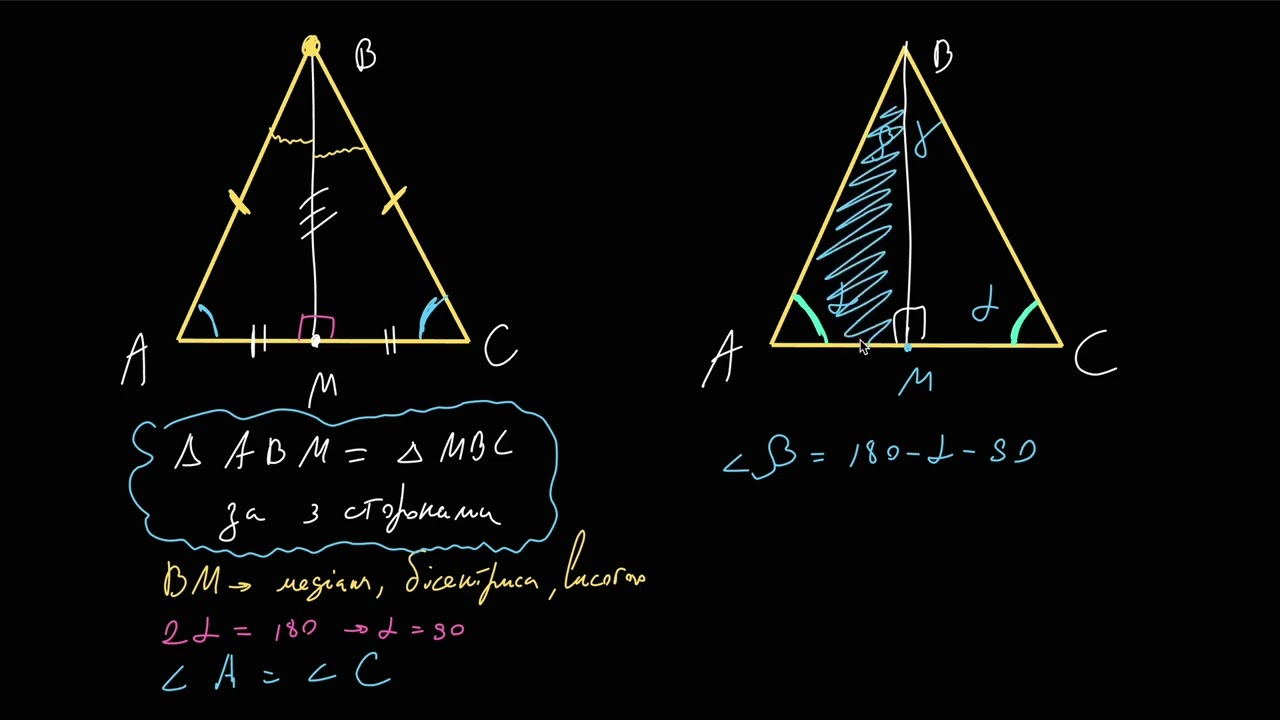Ці приклади демонструють різні способи обчислення. Хтось іде через Піфагора, хтось — через площу. У результаті ми завжди приходимо до точного значення.
М’який заклик: не бійтеся перевіряти задачу кількома методами — це лише зміцнює розуміння.
Поради і типові помилки
Завжди перевіряйте, чи відповідають дані умові існування трикутника.
Не плутайте висоту, проведену до основи, з висотою до бічної сторони.
Використовуйте креслення — навіть простий малюнок зекономить час і нерви.
Приклад. Учень поспіхом рахує, забуває, що висота ділить основу навпіл, і робить помилку. Один малюнок вирішує проблему.
М’який заклик: робіть ескізи, навіть якщо це чернетка — візуалізація допомагає уникати зайвих помилок.
Висота рівнобедреного трикутника — не просто формула, а інструмент, що пов’язує інші елементи фігури. Через неї ми виходимо на площу, кути, медіани.
Колись я бачив, як учень, який довго боровся із задачами, раптом усміхнувся, коли зрозумів просту властивість: висота ділить основу навпіл. Цей момент став для нього «ключем» до цілої теми.
М’який заклик: спробуйте і ви подивитися на висоту як на ключ, а не як на суху лінію. Тоді математика перестане здаватися абстрактною і стане зрозумілою.
